How to Use the Log-Normal Distribution in Python

The log-normal distribution is a continuous probability distribution that is defined as the logarithm of a random variable that follows a normal distribution. This distribution is commonly used in various fields such as finance, physics, engineering, and economics due to its ability to model positively skewed data. In this article, we will discuss the underlying mathematical concept of the log-normal distribution, its properties, alternative approaches, and how to use it in Python.

Mathematical Formulation

Let X be a random variable following a normal distribution with mean μ and standard deviation σ. The log-normal distribution of X is defined as Y = exp(X), where exp is the exponential function. The probability density function (PDF) of Y is given by:

$f_{Y}(y) = \frac{1}{\sigma y \sqrt{2\pi}} e^{-\frac{(\ln(y)-\mu)^2}{2\sigma^2}}$

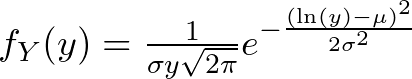
where y > 0. The mean and standard deviation of the log-normal distribution are related to those of the normal distribution through the following equations:

$\mu_{Y} = e^{\mu + \frac{\sigma^2}{2}}$

$\sigma_{Y} = \sigma e^{\mu + \frac{\sigma^2}{2}} \sqrt{\ln(e + \frac{\pi^2}{6})}$

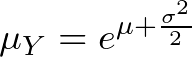
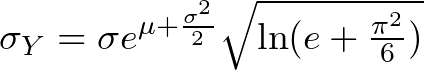
Properties

The log-normal distribution has the following properties:

Positive skewness: The distribution is positively skewed, meaning that the tail extends towards larger values.
Memoryless property: The log-normal distribution has the memoryless property, which means that the future behavior is independent of the past behavior.
Continuous: The distribution is continuous and has an infinite number of possible outcomes.
Unimodal: The distribution is unimodal, meaning that it has a single peak.

Alternative Approaches

There are alternative ways to model positively skewed data, such as the Pareto distribution, the power law distribution, and the Weibull distribution. The choice of distribution depends on the specific problem and the data at hand.

Implementing the Log-Normal Distribution in Python

Python’s SciPy library provides functions to generate and fit log-normal distributions. Here’s an example of how to generate a log-normal distribution with mean μ = 1 and standard deviation σ = 0.5 using the scipy.stats.lognorm module:

import numpy as np
from scipy.stats import lognorm

# Define mean and standard deviation
mu = 1
sigma = 0.5

# Generate log-normal random numbers
x = lognorm.rvs(s=mu, scale=np.exp(sigma), size=10000)

# Plot histogram and log-normal distribution
import matplotlib.pyplot as plt

plt.hist(x, bins=50, density=True, label='Histogram')
plt.plot(np.linspace(x.min(), x.max(), 100), lognorm.pdf(np.linspace(x.min(), x.max(), 100), s=mu, scale=np.exp(sigma)), label='Log-normal Distribution')
plt.legend()
plt.show()

In this example, we generate 10,000 log-normal random numbers and plot their histogram along with the corresponding log-normal distribution. The resulting plot shows the good agreement between the empirical data and the theoretical distribution.

Conclusion

The log-normal distribution is a powerful probability distribution that is widely used to model positively skewed data. In this article, we discussed the underlying mathematical concept of the log-normal distribution, its properties, alternative approaches, and how to use it in Python using the SciPy library. By understanding and implementing the log-normal distribution, you can gain valuable insights into various real-world phenomena and make more informed decisions based on data.

References

Mood, A. M., Graybill, F. A., & Boes, D. C. (1974). Statistical models in engineering science. McGraw-Hill.
Scipy documentation: Log-normal Distribution

On Statistics