How to Calculate and Plot the Normal CDF in Python

The Normal Cumulative Distribution Function (CDF) is an essential concept in statistics and probability theory. It describes the probability that a normally distributed random variable X with mean μ and standard deviation σ takes on a value less than or equal to a given value x. In other words, it returns the probability that X falls below a certain threshold.

There are several ways to calculate and plot the Normal CDF. One common method is using the scipy.stats library in Python. This library provides pre-implemented functions to calculate and plot the Normal CDF.

Mathematical Formulation

The Normal CDF is given by the following mathematical formula:

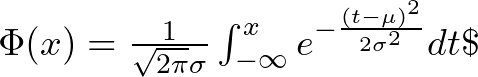
Where:

• is the Normal CDF at x
• is the mean
• is the standard deviation
• is the base of the natural logarithm
• is a variable of integration

Calculating the Normal CDF in Python

To calculate the Normal CDF in Python using the scipy.stats library, simply call the cdf function of the norm distribution object, passing the mean and standard deviation as arguments:

from scipy.stats import norm

# Define mean and standard deviation
mean = 0
stddev = 1

# Calculate Normal CDF at a given value
x = 1.5
cdf_value = norm.cdf(x, loc=mean, scale=stddev)

# Print the result
print(f"The Normal CDF at x = {x} is {cdf_value}")

Plotting the Normal CDF in Python

To plot the Normal CDF using the scipy.stats library, call the ppf function to generate a range of x values, and then plot the Normal CDF against these x values using matplotlib:

import matplotlib.pyplot as plt

# Define mean and standard deviation
mean = 0
stddev = 1

# Generate range of x values
x = np.linspace(-3, 3, 100)

# Calculate Normal CDF at each x value
cdf = norm.cdf(x, loc=mean, scale=stddev)

# Plot the Normal CDF
plt.plot(x, cdf)
plt.xlabel("x")
plt.ylabel("CDF")
plt.show()

The resulting plot will show the Normal CDF for the specified mean and standard deviation:

References

For more information on the Normal Cumulative Distribution Function, please refer to the following resources:

• Wikipedia – Normal Distribution
• Scipy Stats Documentation