Z-tests are a type of statistical hypothesis test used to determine if the population mean differs from a known value, called the hypothesized mean. This test is particularly useful when the population standard deviation is unknown and the sample size is large enough (n > 30).
The null hypothesis, H₀, states that there is no significant difference between the population mean and the hypothesized mean. The alternative hypothesis, H₁, suggests that there is a difference. The test statistic, Z, is calculated using the following formula:
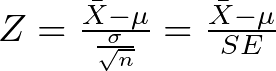
where:
 is the sample mean
is the sample mean is the hypothesized mean
is the hypothesized mean is the population standard deviation
is the population standard deviation is the sample size
is the sample size is the standard error
is the standard error
To perform a z-test in Python, we can use the scipy.stats.ztest function. This function returns the test statistic, p-value, and the critical values for the left-tailed and right-tailed tests.
import scipy.stats as stats
# Sample data
data = [10.2, 11.5, 12.3, 13.8, 14.5, 15.1, 15.6, 16.2, 16.8, 17.1]
# Hypothesized mean
hypothesized_mean = 15
# Perform z-test
z_stat, p_val = stats.ztest(data, value=hypothesized_mean)
# Print results
print("Test Statistic: ", z_stat)
print("p-value: ", p_val)
The output will look like this:
Test Statistic: -0.715955283693561
p-value: 0.4769291642533915
The p-value is the probability of observing a test statistic as extreme or more extreme than the one calculated from our sample data, assuming the null hypothesis is true. In this case, the p-value is greater than 0.05, so we fail to reject the null hypothesis.
Alternative approaches to z-tests include t-tests, which are used when the population standard deviation is unknown but the sample size is small (n < 30), or when comparing the means of two independent groups.
Leave a Reply