In the statistical arena, the paired t-test reigns supreme for analyzing data within the same individuals or units before and after an intervention. But what happens when confounding variables threaten to cloud the true effect? Enter the matched-pairs t-test, a close cousin who steps in as a valiant knight, addressing this challenge by matching individuals across groups. Imagine comparing two teaching methods – the matched-pairs t-test pairs students with similar prior academic performance in each group, isolating the true impact of the methods by controlling for this potentially confounding variable. This article delves into the world of the matched-pairs t-test, equipping you with formulas and insights to leverage its power when tackling confounding variables.
The Challenge of Confounding Variables: When the Paired T-Test Falls Short
Recall the paired t-test: it compares data within the same individuals or units, analyzing the effect of an intervention or change over time. However, sometimes external factors (confounding variables) can influence the observed differences, leading to inaccurate conclusions. For example, in the teaching method example, if students with naturally higher academic performance were assigned to one method, the results might be skewed. Here’s where the matched-pairs t-test steps in, offering a solution.
Formula Focus: Matching for Clarity
The matched-pairs t-test utilizes the same core formula as the paired t-test:
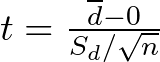
where:
- d̄ is the mean difference between paired observations (e.g., average difference in test scores before and after).
- 0 represents the null hypothesis of no difference (i.e., the mean difference is zero).
- Sd is the standard deviation of the differences between paired observations.
- n is the number of pairs (number of individuals or units).
However, the key difference lies in how pairs are formed:
- Paired t-test: Pairs are simply individuals or units within the same group.
- Matched-pairs t-test: Individuals are matched across groups based on specific criteria (e.g., matching students by prior academic performance). This matching process controls for the confounding variable, isolating the true effect of the intervention.
Unveiling the Significance: Interpreting the P-value’s Message
Similar to other t-tests, the matched-pairs t-test calculates a p-value, indicating the probability of observing such a difference by chance alone. Lower p-values (typically below 0.05) support the rejection of the null hypothesis, suggesting a statistically significant difference between the paired observations, taking into account the matched pairs and thus controlling for the confounding variable.
Beyond the Matching: Unveiling the Full Potential
While addressing confounding variables is its core strength, the matched-pairs t-test offers additional benefits:
- More than two groups: For comparing multiple matched groups, consider one-way ANOVA with matched pairs.
- Non-normally distributed data: If your data doesn’t follow a normal distribution, consider non-parametric alternatives like the Wilcoxon signed-rank test.
Assumptions and Cautions: Matching Comes with Responsibility
Remember, no test is perfect. Here are some key assumptions for the matched-pairs t-test:
- Independence of differences: The differences between paired observations should be independent of each other.
- Normality of differences: Ideally, the differences between paired observations should follow a normal distribution. Check for normality using tests like Shapiro-Wilk or visualize it with histograms.
- Equal variances: The variances of the differences between paired observations should be similar.
Leave a Reply