Imagine observing raindrops hitting your window – you can’t predict exactly when each drop will fall, but you can estimate the overall frequency. This unpredictable yet quantifiable pattern exemplifies the Poisson distribution, a statistical hero adept at modelling discrete events occurring within a fixed time or space. Whether analysing car accidents on a highway or website hits throughout the day, the Poisson distribution unveils the underlying order within the seeming chaos of random events. This article delves into the world of the Poisson, providing diverse examples, exploring its applications, and equipping you with the knowledge to utilize this versatile tool effectively.
Raining Probabilities: Understanding the Core of the Poisson
Think of the Poisson distribution as a raindrop counter, keeping track of individual drops within a defined period (the windowpane). While you can’t predict each specific drop, the average rate of rainfall remains constant. The Poisson distribution leverages this concept, calculating the probability of observing a specific number of events within a fixed interval, given the average rate of occurrence. This predictability makes it ideal for scenarios where events happen independently and randomly, with no “memory” of past occurrences.
Examples Unfurled: Where the Poisson Distribution Counts the Raindrops
The Poisson distribution’s reach extends beyond raindrops, counting diverse events:
- Traffic accidents: Analyze the frequency of accidents on a specific road section per hour, helping assess safety measures.
- Website hits: Track the number of visitors arriving at a website every minute, providing insights into traffic patterns.
- Customer calls: Estimate the number of calls received by a call center in a given timeframe, aiding in resource allocation.
- Biological phenomena: Model the occurrences of mutations in DNA strands or the arrival of customers at a bank during peak hours.
Beyond the Counting: Unveiling the Applications of the Poisson
The Poisson distribution goes beyond mere counting events:
- Predicting probabilities: Calculate the likelihood of observing a specific number of events within a defined interval, aiding in risk assessment.
- Testing hypotheses: Test theories about the average event rate based on observed data, validating safety measures or marketing campaigns.
- Estimating confidence intervals: Quantify the range within which the true average event rate likely lies, providing a margin of error.
Formula Focus: Decoding the Raindrop Counter
The probability of observing “x” events within a fixed interval with an average rate of “λ” is given by:
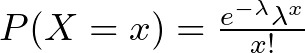
where:
- e is the mathematical constant approximately equal to 2.718.
- λ is the average rate of occurrence (e.g., average number of accidents per hour).
- x! is the factorial of x (product of all positive integers less than or equal to x).
While calculators handle the calculations, understanding the formula provides deeper insights into the rainfall pattern.
Visualizing the Rainfall: Tools for Clarity
Visualizing the Poisson distribution helps comprehend the event frequency:
- Probability mass function (PMF): A bar chart with bars at each possible number of events, depicting their respective probabilities.
- Cumulative distribution function (CDF): A graph showing the probability of encountering less than or equal to a certain number of events, helping identify periods with higher or lower activity.
Beyond the Randomness: Considerations and Limitations
Remember, the Poisson distribution thrives on independent, random events with a constant average rate. Deviations require alternative approaches:
- Clustering events: If events tend to occur in bursts, consider alternative models like the negative binomial distribution.
- Non-constant rate: If the event rate changes over time or space, consider Poisson processes with time-varying rates.
Leave a Reply