In statistics, where data follows various distributions, normality, characterized by the familiar bell curve, holds an important position. However, not all data adheres to this pattern. This article explores the Shapiro-Wilk test, a statistical tool designed to evaluate whether your data aligns with the normal distribution.
Understanding the Concept of Normality:
Imagine measuring people’s heights in a population. Heights wouldn’t be identical; some would be taller, some shorter, forming a bell-shaped curve with most individuals clustered around the average, and fewer at the extremes. This represents a normal distribution with specific mathematical properties. Data closely resembling this curve is considered normally distributed.
Why Normality Matters:
Many statistical tests, including t-tests, ANOVA, and linear regression, rely on the assumption of normality for accurate results. When data deviates significantly, these tests might produce misleading conclusions.
Introducing the Shapiro-Wilk Test:
While visual tools like histograms and Q-Q plots offer hints, the Shapiro-Wilk test formally assesses normality. It compares the observed distribution of your data to the theoretical normal distribution using a statistic called the W-statistic.
Understanding the Formula:
The Shapiro-Wilk statistic (W) is calculated based on the ordered values of your data (x₁, x₂, …, xn) and their expected values under normality (μi):
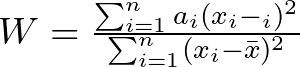
where:
- a_i are coefficients specific to the sample size (n) and calculated beforehand.
- μ_i are the expected values of x_i under normality, estimated from the data.
- x̄ is the sample mean.
Higher W values indicate closer resemblance to normality, with values greater than 0.95 often considered evidence of normality.
Interpreting the Results:
The Shapiro-Wilk test also calculates a p-value, indicating the probability of observing such a W-statistic by chance, assuming normality. Lower p-values (typically below 0.05) suggest rejecting the null hypothesis (data is not normally distributed).
Important Considerations:
Remember, no test is perfect:
- Sample size: The Shapiro-Wilk test performs best with larger sample sizes (n > 50). For smaller samples, consider alternative tests like Shapiro-Francia or Kolmogorov-Smirnov.
- Normality deviations: The test is sensitive to specific deviations from normality, like outliers or skewness. Consider visual inspection and transformations before relying solely on the p-value.
Leave a Reply