On Statistics

Confidence Intervals for the Difference Between Means

In the realm of data analysis, comparing two populations or groups often lies at the heart of our inquiries. Whether it’s examining the effectiveness of different teaching methods, assessing the growth rates of two companies, or comparing the average age of residents in two neighbourhoods, understanding the difference between the populations becomes crucial. However, relying solely on the point estimates, like the means of each group, can be misleading, as they fail to account for the inherent variability in sample data. This is where confidence intervals for the difference between means come to the rescue, painting a more comprehensive picture of the potential gap between the population means.

What is a Confidence Interval for the Difference Between Means?

Similar to the confidence interval for a single mean, this statistical tool constructs a range of plausible values for the difference between the population means with a specified level of confidence. This range, expressed as a lower and upper bound, helps us quantify the uncertainty associated with our estimated difference and assess the likelihood of a true difference existing between the populations.

Formulating the Confidence Interval: Unveiling the Mechanics

The construction of this confidence interval hinges on several key elements:

  • Sample means (x̄₁ and x̄₂): These represent the average values calculated from the respective samples drawn from the two populations.
  • Standard deviations (σ₁ and σ₂): These reflect the spread of data within each population.
  • Sample sizes (n₁ and n₂): The number of observations in each sample.
  • Standard error (SE) of the difference in means: This crucial metric captures the variability associated with the estimated difference and is calculated based on the aforementioned elements.

The general formula for the confidence interval for the difference between means takes the following form:

Lower Bound = (x̄₁ - x̄₂) ± ME Upper Bound = (x̄₁ - x̄₂) ± ME

where ME represents the margin of error, which is calculated based on the chosen confidence level (1-α) and the standard error (SE) of the difference in means.

Choosing the Formula: Navigating Different Scenarios

Depending on the sampling approach and the knowledge about population parameters, different formulas are employed to calculate the standard error (SE):

1. Independent samples and known population standard deviations (σ₁ and σ₂):

SE = \sqrt{\left(\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}\right)}

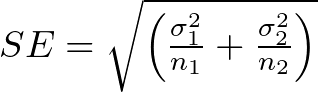
2. Independent samples and unknown population standard deviations (σ₁ and σ₂), but known population variances (σ₁² and σ₂²):

SE = \sqrt{\left( \frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2} \right)}

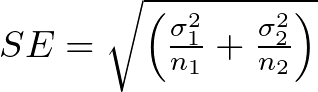
3. Independent samples and unknown population standard deviations (σ₁ and σ₂):

SE = \sqrt{\left( \frac{s_1^2}{n_1} + \frac{s_2^2}{n_2} \right) \cdot \frac{(n_1 - 1) + (n_2 - 1)}{n_1 + n_2 - 2}}

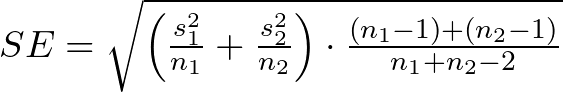
where:

  • s₁ and s₂ are the sample standard deviations of the respective samples.
  • n₁ and n₂ are the sample sizes.

4. Paired samples (dependent):

SE = \sqrt{\left( \frac{\sum_{i=1}^{n} d_i^2}{n - 1} \right)}

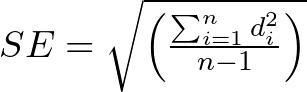
where:

  • d is the difference between the paired observations.
  • n is the number of pairs.

Interpreting Confidence Intervals: A Case Study

Imagine we are comparing the average exam scores of students taught by two different teaching methods. We randomly select 20 students from each group (n₁ = n₂ = 20) and obtain the following results:

  • Group 1 (Method A): Mean score (x̄₁) = 78, Standard deviation (s₁) = 5
  • Group 2 (Method B): Mean score (x̄₂) = 82, Standard deviation (s₂) = 4

We are interested in constructing a 95% confidence interval to estimate the true difference in the average exam scores between students taught by the two methods.

Choosing the Formula:

Since the samples are independent and the population standard deviations are unknown, we will utilize formula 3. Calculating the necessary components, we get:

  • SE ≈ 2.22

Constructing the Confidence Interval:

Lower Bound = (78 – 82) ± 2.22 ≈ -6.22 Upper Bound = (78 – 82) ± 2.22 ≈ -1.78

Interpretation:

With a 95% level of confidence, we can conclude that the true average difference in exam scores between students taught by the two methods falls within the range of -6.22 and -1.78 points.

Leave a Reply

Your email address will not be published. Required fields are marked *