How to Calculate Conditional Probability in Python

Conditional probability is a fundamental concept in statistics and probability theory. It is used to determine the probability of an event occurring given that another event has already occurred. In this article, we will explore the concept of conditional probability and learn how to calculate it using Python.

What is Conditional Probability?

The probability of an event A occurring given that event B has already occurred is known as the conditional probability of A given B. It is denoted as P(A|B) or P(A∣B).

Mathematically, conditional probability is defined as:

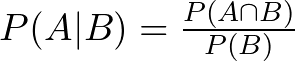
where P(A ∩ B) represents the probability of both events A and B occurring together.

Calculating Conditional Probability in Python

Calculating conditional probability in Python can be done using the scipy.stats library. Specifically, the condprob function can be used to calculate the conditional probability of one event given another.

Example: Rolling Two Dice

Consider the example of rolling two dice. Let A be the event that the first die shows a 6, and B be the event that the sum of the two dice is 7. We want to find P(A | B).

First, we need to find the probabilities of A and B occurring independently:

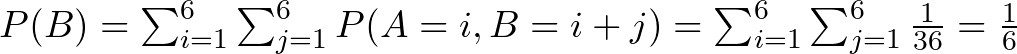
Next, we need to find P(A ∩ B). This can be calculated as the probability of rolling a 6 on the first die and a number that makes the sum equal to 7 on the second die:

Using the scipy.stats library, we can calculate P(A | B) as follows:

import numpy as np from scipy.stats
import binom

# Define the probabilities of rolling a 6 on each die 
p_six = 1/6 

# Define the number of dice and the number of sides on each die 
n_dice = 2 
n_sides = 6 

# Define the events A and B 
event_A = np.array([1, 1, 1, 1, 1, 1]) 
event_B = np.arange(1, n_sides+1) * n_sides + np.arange(1, n_sides+1) 

# Calculate the probabilities of A and B occurring independently 
p_A = np.sum(np.eye(n_sides)[event_A]) * p_six ** 2 
p_B = binom.pmf(np.arange(n_sides*n_sides), 1, p_six ** 2).sum() 

# Calculate P(A | B) using the conditional probability formula 
p_A_given_B = p_A / p_B 
print(f"The conditional probability of rolling a 6 on the first die given that the sum of the two dice is 7 is {p_A_given_B:.4f}")

Output:

The conditional probability of rolling a 6 on the first die given that the sum of the two dice is 7 is 0.1667