How to Calculate Spearman Rank Correlation in Python

Spearman rank correlation is a statistical method used to measure the strength and direction of association between two variables. Unlike Pearson correlation, which assumes a linear relationship between variables, Spearman rank correlation considers monotonic relationships, meaning that the relationship can be either increasing or decreasing.

The Spearman rank correlation coefficient, denoted by ρ (rho), is calculated based on the ranks of the data points rather than their actual values. It ranges from -1 to 1, where -1 indicates a perfect negative correlation, 0 indicates no correlation, and 1 indicates a perfect positive correlation.

Mathematically, the Spearman rank correlation coefficient can be calculated using the following formula:

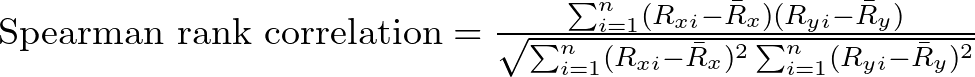
Python implementation

Here’s how to calculate Spearman rank correlation coefficient in Python using the scipy.stats library:

import numpy as np
from scipy.stats import spearmanr

# Generate some random data
x = np.random.randint(1, 11, size=100)
y = np.random.randint(1, 11, size=100)

# Calculate Spearman rank correlation coefficient
result = spearmanr(x, y)

# Print the correlation coefficient and p-value
print("Spearman's rho: ", result.correlation)
print("p-value: ", result.pvalue) 

The output will look like:

Spearman's rho:  0.1738814131151885
p-value:  0.01659932811552736

In this example, the Spearman rank correlation coefficient is 0.1739, indicating a weak positive association between the two variables.