How to Perform Z-Tests in Python

Z-tests are a type of statistical hypothesis test used to determine if the population mean differs from a known value, called the hypothesized mean. This test is particularly useful when the population standard deviation is unknown and the sample size is large enough (n > 30).

The null hypothesis, H₀, states that there is no significant difference between the population mean and the hypothesized mean. The alternative hypothesis, H₁, suggests that there is a difference. The test statistic, Z, is calculated using the following formula:

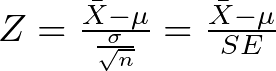
where:

• is the sample mean
• is the hypothesized mean
• is the population standard deviation
• is the sample size
• is the standard error

To perform a z-test in Python, we can use the scipy.stats.ztest function. This function returns the test statistic, p-value, and the critical values for the left-tailed and right-tailed tests.

import scipy.stats as stats

# Sample data
data = [10.2, 11.5, 12.3, 13.8, 14.5, 15.1, 15.6, 16.2, 16.8, 17.1]

# Hypothesized mean
hypothesized_mean = 15

# Perform z-test
z_stat, p_val = stats.ztest(data, value=hypothesized_mean)

# Print results
print("Test Statistic: ", z_stat)
print("p-value: ", p_val)

The output will look like this:

Test Statistic:  -0.715955283693561
p-value:  0.4769291642533915

The p-value is the probability of observing a test statistic as extreme or more extreme than the one calculated from our sample data, assuming the null hypothesis is true. In this case, the p-value is greater than 0.05, so we fail to reject the null hypothesis.

Alternative approaches to z-tests include t-tests, which are used when the population standard deviation is unknown but the sample size is small (n < 30), or when comparing the means of two independent groups.