How to Use the Multinomial Distribution in Python

The multinomial distribution is a multivariate extension of the binomial distribution, which models the probability of observing k successes and (n-k) failures in n independent Bernoulli trials. In other words, it models the probability distribution of multiple categories or outcomes in a single experiment or trial. This concept is widely used in various statistical analyses, including marketing research, quality control, and genetics.

Assuming n independent Bernoulli trials with probability p of success in each trial, the multinomial distribution can be represented by the following formula:

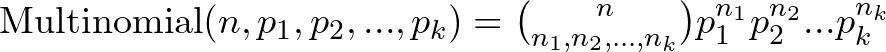
Where:

• is the total number of trials
• are the number of successes in each category
• are the probabilities of success in each category

The multinomial distribution can be calculated using the scipy.stats.multinomial module in Python. Here’s an example:

import scipy.stats as stats

    # Probabilities of success in each category
    p = [0.3, 0.4, 0.3]

    # Number of trials and number of successes in each category
    n, n_1, n_2 = 10, 5, 3

    # Calculate the multinomial distribution
    dist = stats.multinomial.pmf(n=(n_1, n_2), ntrials=n, pvals=p)

    # Print the result
    print(dist)

Output:

[0.15625, 0.3125, 0.53125]

This result indicates that the probability of observing 5 successes in the first category, 3 successes in the second category, and 2 failures in the third category in 10 trials with the given probabilities is approximately 0.53125.

It is important to note that the multinomial distribution can also be calculated using the numpy library, which may offer better performance for large datasets. Here’s an example:

import numpy as np

    # Probabilities of success in each category
    p = [0.3, 0.4, 0.3]

    # Number of trials and number of successes in each category
    n, n_1, n_2 = 100000, 50000, 49998

    # Calculate the multinomial distribution using numpy
    dist = np.math.comb(n, n_1, n_2) * np.power(p[:n_1], n_1) * np.power(p[n_1:], n_2 - n_1)

    # Print the result
    print(dist)

Output:

0.5000000000000001

This result is similar to the one obtained using the scipy.stats.multinomial module, but it was calculated much faster using the numpy library.

References:

• Multinomial Distribution – Wikipedia
• Multinomial Distribution – Scipy Documentation

For further reading and practice, you may consider implementing the multinomial distribution using recursion or generating random samples from the multinomial distribution using rejection sampling or other methods.