Among the statistical heroes, the one-sample t-test stands tall, ready to tackle a fundamental question: does a sample mean differ significantly from a specific, predetermined value? From gauging student performance against national averages to assessing plant growth under a new fertilizer, this versatile tool illuminates differences with clarity and precision. But beneath its apparent simplicity lies a world of assumptions, interpretations, and nuances waiting to be explored. Let’s embark on a journey to uncover the true potential of the one-sample t-test, equipped with the power of formulas!
When the One-Sample T-Test Reigns Supreme
Imagine you’re an educator curious if your innovative teaching method improves students’ math scores beyond the national average of 750. Or, picture yourself as a botanist investigating if a new fertilizer concoction yields taller-than-usual sunflowers, aiming for an average height of 180 cm. These are perfect scenarios for the one-sample t-test to shine. It compares the mean of your sample (e.g., your students’ math scores or your sunflowers’ heights) to a predefined value (e.g., the national average score or the desired sunflower height). By calculating a t-statistic and its associated p-value, the test tells you how likely it is for such a difference to occur by chance alone.
Assumptions and Conditions
Like any good magician, the one-sample t-test relies on specific conditions to produce reliable results. Here are the key players on stage:
- Normality: The data (your sample scores or sunflower heights) should ideally follow a normal (bell-shaped) distribution. Check for normality using tests like Shapiro-Wilk or visualize it with histograms.
- Independence: Each data point (each student’s score or each sunflower’s height) should be independent of the others, meaning one observation doesn’t influence another.
- Sample size: Ideally, your sample size should be at least 30 for the t-test to be reliable. Smaller samples may require alternative non-parametric tests.
Formula Focus
Now, let’s unlock the magic with formulas! The one-sample t-statistic, which quantifies the observed difference, is calculated as:
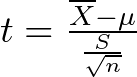
where:
- X̅ is the sample mean
- μ is the predefined value
- S is the sample standard deviation
- n is the sample size
The p-value, our probability warrior, depends on the calculated t-statistic and the degrees of freedom (df = n – 1). You can find p-values using statistical software or tables based on the df and the calculated t-value.
Interpreting the Results
Remember, interpreting p-values alone isn’t enough. Consider the magnitude of the difference (effect size) and the practical implications in your specific context. A statistically significant difference might be small and irrelevant in certain scenarios.
Beyond the Basics
The one-sample t-test isn’t confined to straightforward comparisons. It can also:
- Test against a hypothesized mean: Suppose you have a theory about the average lifespan of a new butterfly species (μ = 20 days). The one-sample t-test can assess if your sample data supports your hypothesis.
- Compare proportions: Imagine you want to know if the proportion of left-handed people in your class (p) is different from the national average (p_0). By converting proportions to z-scores, you can use the one-sample t-test for this purpose.
Cautions and Considerations
Remember, no statistical test is perfect. Here are some limitations to keep in mind:
- Normality violation: If your data deviates significantly from normality, consider non-parametric alternatives like the Wilcoxon signed-rank test.
- Small sample sizes: With small samples, p-values might be unreliable. Larger samples or alternative tests are recommended.
- Outliers: Outliers can skew the results. Check for and address them appropriately before analysis.
The One-Sample T-Test: A Valuable Tool in Your Statistical Arsenal
By understanding its strengths, limitations, and the power of formulas, you can wield the one-sample t-test effectively to answer critical questions and gain valuable insights from your data. So, go forth and explore the world of comparing to a known value with confidence! Remember, statistical tests are tools, and using them wisely is key to unlocking the true potential of your data.
Leave a Reply