How to Use the Poisson Distribution in Python

What is the Poisson Distribution?

The Poisson distribution is a discrete probability distribution that models the probability of a given number of events occurring in a fixed interval of time or space, given the average rate of occurrence of the events. It is often used when the number of occurrences is small and the events occur independently of each other. The probability mass function (PMF) of the Poisson distribution is given by:

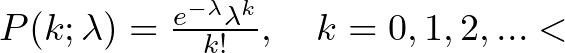
where is the average rate of occurrence of the events in the interval.

Alternative Approaches

There are other probability distributions that can be used to model counting processes, such as the binomial distribution and the negative binomial distribution. The choice of distribution depends on the specific problem at hand.

Implementing the Poisson Distribution in Python

Python’s scipy.stats module provides a function called poisson that can be used to calculate the PMF of the Poisson distribution. Here’s an example:

import numpy as np
from scipy.stats import poisson

# Set the average rate of occurrence
lambda_ = 3

# Generate some numbers of occurrences to calculate the PMF for
k = np.arange(0, 11)

# Calculate the PMF using the poisson function
p = poisson.pmf(k, lambda_)

# Print the PMF
print(p)

Output:

[0.04981865 0.10983363 0.13591402 0.15073068 0.15121242 0.14298855 0.12757895 0.0983353  0.06689595 0.03926997]