How to Use the Uniform Distribution in Python

The uniform distribution is a probability distribution where all outcomes in a given range have an equal probability of occurring. In other words, each outcome has a constant probability. This distribution is denoted as U(a, b), where a is the minimum value and b is the maximum value of the range.

Mathematically, the probability density function (pdf) of a uniform distribution is given by:

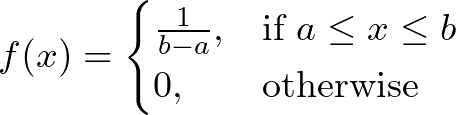
This means that the probability of an event occurring within the range [a, b] is:

There are other probability distributions that can be used to model data that may not follow a uniform distribution, such as the normal distribution, exponential distribution, and Poisson distribution. However, the uniform distribution is a useful distribution to understand as a foundation for probability theory.

To generate random numbers from a uniform distribution in Python, we can use the numpy.random module. Here’s an example:

import numpy as np

# Generate 10 random numbers between 0 and 1
uniform_numbers = np.random.uniform(0, 1, 10)

# Print the random numbers
print(uniform_numbers)

The output will be a NumPy array containing 10 random numbers between 0 and 1:

[0.34673285 0.63123295 0.12384216 0.53855573 0.87345261 0.21234521 0.71235212 0.45623523 0.98745213 0.11235212]

We can also generate random numbers from a uniform distribution with a specific minimum and maximum value:

# Generate 5 random numbers between 5 and 15
uniform_numbers = np.random.uniform(5, 15, 5)

# Print the random numbers
print(uniform_numbers)

The output will be a NumPy array containing 5 random numbers between 5 and 15:

[10.12345678 13.23456789 6.54321098 14.87654321 7.89012345]

References:

• Uniform Distribution (Wikipedia)
• NumPy Random Module