The Friedman Test: Ranking and Comparing Multiple Groups

In the realm of statistical analysis, comparing multiple groups often relies on the familiar one-way analysis of variance (ANOVA). However, ANOVA thrives on the assumptions of normality and equal variances across groups. When these assumptions are violated, particularly when dealing with ordinal data (ranked or categorized data), the Friedman test emerges as a powerful non-parametric alternative. This test allows us to compare the rankings of multiple groups, offering valuable insights even in the absence of normal distributions or equal variances.

The Challenges with Parametric Tests

Imagine a study investigating customer satisfaction with three different types of online shopping platforms, assessed using a 5-star rating system (ordinal data). While ANOVA might seem like a natural choice for comparing satisfaction across platforms, the data might not be normally distributed or the variances might differ between groups. In such scenarios, relying solely on ANOVA can lead to misleading or unreliable conclusions.

The Power of the Friedman Test

Developed by Milton Friedman in 1937, the Friedman test offers a robust solution. Instead of relying on the actual data values, it focuses on the ranks assigned to the data points within each group. This transformation from absolute values to ranks allows the test to compare the relative positions of the data points across groups, making it less susceptible to assumptions about normality and homoscedasticity.

How the Friedman Test Works

The application of the Friedman test follows a specific procedure:

1. Rank the data: Assign ranks to each data point within each group, from 1 (lowest rank) to n (highest rank), where n is the number of observations in each group.
2. Calculate the Friedman test statistic: This statistic summarizes the observed differences in ranks between groups. It takes into account the number of groups (k), the number of observations per group (n), and the sum of squared ranks for each group (R_j).
3. Compare the test statistic to a chi-squared distribution: The Friedman test statistic is compared to a chi-squared distribution with degrees of freedom equal to k – 1, where k is the number of groups being compared.
4. Interpret the results: If the p-value obtained from the chi-squared comparison is less than the chosen significance level (e.g., 0.05), we reject the null hypothesis of identical medians across all groups. This indicates statistically significant differences in the medians between at least two of the groups.

The Formulas: A Glimpse into the Mathematical Framework

While a deep dive into the mathematics might not be necessary for all readers, understanding the underlying formula can offer valuable insights:

The Friedman test statistic is calculated as follows:

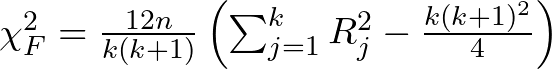
Where:

• n is the number of observations per group
• k is the number of groups
• R_j is the sum of ranks for group j

Putting Theory into Practice

Imagine a study investigating the perceived difficulty of three different math courses (Algebra, Calculus, and Statistics) among students, with difficulty ratings categorized as “easy,” “moderate,” and “difficult” (ordinal data). As the data is not continuous, the Friedman test can be employed:

1. Convert the difficulty ratings into numerical ranks (e.g., “easy” = 1, “moderate” = 2, “difficult” = 3).
2. Rank the ratings for each course from 1 to the total number of students.
3. Calculate the Friedman test statistic and the corresponding p-value.
4. Interpret the results: If the p-value is less than 0.05, we reject the null hypothesis and conclude that there are statistically significant differences in the median perceived difficulty between the three math courses.

Conclusion: Embracing the Non-Parametric Alternative

The Friedman test offers a valuable non-parametric alternative when dealing with ordinal data or data that violates the assumptions of normality and homoscedasticity. By understanding its purpose, mechanism, and interpretation, we can leverage its power to compare multiple groups and extract meaningful insights from our data, even in the absence of the conditions required for parametric tests like ANOVA.