In the captivating saga of statistical tests, the pooled t-test emerges as a unifying force, combining the variances of two independent groups under a crucial assumption: homogeneity of variances. Imagine comparing the effectiveness of two fertilizers on plant growth – if both groups exhibit similar variability in growth (equal variances), the pooled t-test offers superior power compared to its individual counterparts. This article delves into the world of the pooled t-test, equipping you with formulas and insights to leverage its unifying power when the conditions are right.
Recall the independent two-sample t-test: it compares the means of two independent groups, assuming equal variances. However, this assumption can sometimes be violated, leading to inflated Type I error (incorrectly rejecting the null hypothesis) and reduced power to detect true differences. Enter the pooled t-test, a valiant knight ready to address this challenge by combining the variances of both groups when their homogeneity is confirmed.
Formula Focus
The pooled t-test wields a formula similar to the independent two-sample t-test, with a key difference in the variance term:
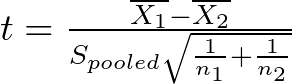
where:
- X̅₁ and X̅₂ are the sample means of Groups 1 and 2, respectively.
- Spooled is the pooled standard deviation, calculated using the variances of both groups:
![Rendered by QuickLaTeX.com S_{pooled}^2 = \dfrac{[(n_1 - 1) \cdot S_1^2 + (n_2 - 1) \cdot S_2^2]}{(n_1 + n_2 - 2)}](https://onstatistics.com/wp-content/ql-cache/quicklatex.com-4492468ba0e2b7cb2df78d3efd30068a_l3.png)
- n₁ and n₂ are the sample sizes of Groups 1 and 2, respectively.
This pooled variance provides a more robust estimate of variability, leading to a more powerful t-statistic and, consequently, a higher chance of detecting true differences between the means when they exist.
Interpreting the P-value’s Message
Similar to other t-tests, the pooled t-test calculates a p-value, indicating the probability of observing such a difference by chance alone. Lower p-values (typically below 0.05) support the rejection of the null hypothesis, suggesting a statistically significant difference between the means. However, remember that this analysis relies on the crucial assumption of homogeneity of variances.
Beyond the Unification
While the pooled t-test thrives on homogeneity, its potential extends beyond:
- Welch’s t-test: When variances significantly differ, Welch’s t-test offers a reliable alternative that doesn’t rely on this assumption.
- Paired t-test: For analyzing data within the same individuals or units before and after an intervention, the paired t-test provides a more suitable approach.
Assumptions and Cautions
Remember, no test is perfect. Here are some critical assumptions for the pooled t-test:
- Homogeneity of variances: This is the foundation of the pooled t-test. Use tests like Levene’s test or visually compare variances to assess its validity.
- Normality of data within each group: Ideally, data within each group should follow a normal (bell-shaped) distribution. Check for normality using tests like Shapiro-Wilk or visualize it with histograms.
- Independence of observations: Observations within each group and between groups should be independent.
Leave a Reply